Contoh SOAL

GETARAN 

Getaran adalah gerak bolak-balik suatu partikel secara periodik melalui titik setimbangnya.

Jika ujung mistar bergerak dari O ke A, lalu ke B, dan kembali ke O (disingkat O – A – O – B – O), dikatakan ujung mistar telah menempuh satu getaran.

Contoh yang lain : A – O – B – O – A atau B – O – A – O – B
Gerak ujung mistar O – A – O ,  O – B – O,  B – O – A,  A – O – B adalah setengah getaran.

Jarak yang ditempuh ujung mistar dari titik seimbangnya disebut simpangan. Jarak O – A dan O – B adalah simpangan terbesar (amplitudo).

Getaran pada bandul

Getaran pada Pegas

Periode dan Frekuensi

Periode didefinisikan sebagai selang waktu yang diperlukan untuk menempuh satu kali getaran. Satuan periode dalam sekon.
Rumus periode :

T = periode (sekon)
t = waktu yang diperlukan untuk melakukan getaran (sekon)
n = banyaknya getaran


Contoh :
Sebuah bandul digetarkan sehingga selama 1 menit menghasilkan 40 getaran. Tentukan periodenya?
Penyelesaian :
Diketahui :
t  = 1 menit = 60 s
n = 40 getaran

Ditanya : T = ?
Jawab :

Merancang eksperimen
Gunakan sebuah ayunan sederhana untuk menyelidiki apakah periode getaran tergantung pada :
a. amplitudo
b. massa beban
c. panjang tali
Jika percobaan dilakukan secara benar, akan diperoleh kesimpulan sebagai berikut :

1. periode tidak tergantung pada amplitudo
2. periode tidak tergantung pada massa beban
3. periode tergantung pada panjang tali

Frekuensi didefinisikan sebagai banyaknya getaran yang dilakukan benda dalam satu sekon. Satuan frekuensi dalam Hertz (Hz).
Rumus frekuensi :

f = frekuensi (Hz)

Contoh soal :
Sebuah bandul selama 20 detik mengalami  30 getaran. Tentukan frekuensinya?
Penyelesaian :
Diketahui :
t  = 20 s
n = 30 getaran
Ditanya : f = ?
Jawab :
f=n/t
T=30/20=1,5 Hz


Hubungan periode dan frekuensi

f=1/T atau T=1/f

Contoh soal :
Sebuah pegas menghasilkan frekuensi 50 Hz. Tentukan periode getaran itu?
Penyelesaian :
Diketahui : f = 50 Hz
Ditanya : T = ?
Jawab :
 T=1/f=1/50=0,02 s

GELOMBANG 

Perhatikan gambar berikut

Jika dalam waktu 1,2 s terjadi gelombang transversal seperti gambar. Tentukan :

a. Panjang gelombang

b. Periode gelombang

c. Cepat rambat gelombang

Penyelesaian :

Diketahui :

l = 10 m

t = 1,2 s

a. Panjang gelombang

    Satu bukit gelombang sama dengan setengah gelombang.

    Jadi, l = ½ λ

    λ= 2 l = 2. 10 = 20 cm

b. Periode gelombang
     Selama 1,2 sekon  terjadi 1,5 gelombang (n = 1,5)

     









BUNYI

1.   Duah buah Garputala bergetar secara bersama-sama dengan frekuensi masing-masing 416 Hz dan 418 Hz
Penyelesaian
Diketahui    :
f1    =  416 Hz
f2    =  418 Hz
Ditanya    :
    fl
    Tl
Jawab
    fl        =  f2 –f1
=  418 – 416
=  2 Hz
    Tl        =  1/fl   
        =  1/2 detik   

2.    Sebuah mesin jahit yang sedang bekerja mempunyai intensitas bunyi 10-8 W/m2. Apabila intensitas ambang bunyi 10-12 wb/m2, hitunglah Taraf intensitas bunyi dari 10 mesin jahit sejenis yang sedang bekerja bersama-sama !
Penyelesaian
Diketahui    :
I1    =  10-8 Watt/m2
Io    =  10-12 Watt/m2
Ditanya    :  TI10 
Jawab        :
TI10    =   10 log I_10/Io             I10   = 10.I1  =  10.10-8  =  10-7 Watt/m2
    =  10 log 〖10〗^(-7)/〖 10〗^(-12)
       =  10 (log 10-7 – log 10-12)
    =  10 (-7 + 12)
    =  10. 5
    =  50 dB

 3.   Pemancar Radio yang berfrekuensi 10.000 Hz mempunyai Panjang gelombang 150 cm. tentukan Cepat rambat bunyi tersebut !
Penyelesaian
Diketahui    :
f    =  10.000 Hz
λ    =  150 cm  = 1,5 m
Ditanya    :  V
Jawab
V    =  λ. f
    =  1,5. 10.000
    =  15.000 m/s
4.    Suatu sumber bunyi bergerak menjauhi seorang Pendengar yang tidak bergerak dengan kecepatan 108 km/jam. Apabila frekuensinya 120 Hz dan Cepat rambat bunyi di udara 340 m/s, tentukanlah frekuensi yang terdengar oleh Pendengar !
Penyelesaian
Diketahui    :
VP    =  0
VS    =  108 km/jam  =  108.000/3600  =  30 m/s
fS    =  120 Hz
V    =  340 m/s
Ditanya    :  fP 
Jawab
fP    =  (V ± V_P)/(V ±V_s ) .fS
    =  (V+ V_P)/(V+ V_S ) . fS
    =  (340+0)/(340+30) . 120
    =  110,27 Hz

CONTOH SOAL SISTEM DIGITAL

1.  Konversi bilangan desimal ke biner Nilai bilangan desimal dibagi dengan 2, pembacaan nilai akhir hasil pembagian dan urutan sisa hasil pembagian adalah bentuk bilangan biner dari nilai desimal.
Contoh soal :
Ubah bilangan desimal 10 ke bilangan biner ?

Jadi bilangan biner untuk bilangan desimal 10 adalah 1010

2. Konversi bilangan biner ke bilangan desimal
Setiap urutan nilai bilangan biner dijumlahkan, dengan terlebih dahulu nilai biner tersebut dikalikan dengan bobot masing – masing bilangan biner.
Contoh soal :
Ubah bilangan biner 1010 ke bilangan desimal ?

Jadi bilangan desimal untuk bilangan biner 1010 adalah 10

3. Konversi bilangan desimal ke bilangan oktal
Nilai bilangan desimal dibagi dengan 8, pembacaan nilai akhir hasil pembagian dan urutan sisa hasil pembagian adalah hasil bilangan oktal dari bilangan desimal.
Contoh soal :
Ubah bilangan desimal 529 ke bilangan oktal ?

Jadi bilangan oktal untuk bilangan desimal 529 adalah 1021

4. Konversi bilangan oktal ke bilangan desimal
Setiap nilai urutan bilangan oktal dijumlahkan, dengan terlebih dahulu nilai oktal tersebut dikalikan dengan bobot masing –masing bilangan oktal.
Contoh soal :
Ubah bilangan oktal 1021 ke bilangan desimal ?

Jadi bilangan desimal untuk bilangan oktal 1021 adalah 529

5. Konversi bilangan desimal ke bilangan heksadesimal
Konversi bilangan desimal ke bilangan heksadesimal dapat dilakukan dengan cara yang sama seperti cara sebelumnya dengan melakukan pembagian bilangan desimal dengan 16 sehingga sisa dan urutan sisanya adalah hasil bilangan heksadesimal.
Untuk ini akan digunakan cara lain agar dapat menambah referensi dan ilmu pengetahuan.
Contoh soal :
Ubah bilangan desimal 5052 ke bilangan heksadesimal ?

Jadi bilangan heksadesimal untuk bilangan desimal 5052 adalah 13BC

6. Konversi bilangan heksadesimal ke bilangan desimal
Dengan melakukan cek kebenaran hasil sebelumnya dapat diketahui hasil bilangan desimal tersebut. Dapat dilakukan dengan cara yang sama seperti konversi – konversi sebelumnya untuk mendapatkan bentuk bilangan desimal.
Contoh soal :
Ubah bilangan heksadesimal 13BC ke bilangan desimal ?

Jadi bilangan desimal untuk bilangan heksadesimal 13BC adalah 5052

7. Konversi bilangan oktal ke bilangan biner
Setiap digit bilagan oktal dapat direpresentasikan ke dalam 3 digit bilangan biner. Setiap digit bilangan oktal diubah secara terpisah.
Contoh soal :
Ubah bilangan oktal 4567 ke bilangan biner ?

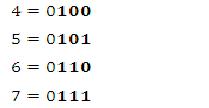
Yang diambil adalah 3 digit terakhir atau yang tercetak hitam.
Jadi bilangan biner untuk bilangan oktal 4567 adalah 100 101 110 111

8. Konversi bilangan biner ke bilangan oktal
Pengelompokan setiap tiga digit bilangan biner mulai dari LSB hingga MSB. Setiap kelompok akan menandakan nilai oktal dari bilangan tersebut.
Contoh soal :
Ubah bilangan biner 11110011001 ke bilangan oktal ?
Langkah pertama adalah bagi bilangan biner tersebut menjadi 3 digit

Langkah kedua adalah mengganti bilangan biner

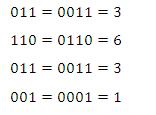
Jadi blangan oktal untuk bilangan biner 11110011001 adalah 3631

9. Konversi bilangan heksadesimal ke bilangan biner
Setiap digit bilangan heksadesimal dapat direpresentasikan ke dalam 4 digit bilangan biner. Setiap digit bilangan heksadesimal diubah secara terpisah.
Contoh soal :
Ubah bilangan heksadesimal 2AC ke bilangan biner ?

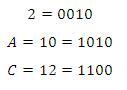
Jadi bilangan biner untuk bilangan heksadesimal 2AC adalah 0010 1010 1100

10.  Konversi bilangan biner ke bilangan heksadesimal
Pengelompokan setiap empat digit bilangan biner mulai dari LSB hingga MSB . setiap kelompok akan menandakan nilai heksa dari bilangan tersebut.
Contoh soal :
Ubah bilangan biner 0010 1010 1100 ke bilangan heksadesimal ?

Jadi bilangan heksadesimal untuk bilangan biner 0010 1010 1100 adalah 2AC
Contoh soal 2 :
Ubah bilangan biner 10011110101 ke bilangan heksadesimal ?

Jadi bilangan heksadesimal untuk bilangan biner 10011110101 adalah 4F
semoga artikel diatas dapat bermanfaat dan bisa digunakan untuk referensi belajar.